Khosla’s Method of independent variables for determination of pressures and exit gradient for seepage below a weir or a barrage
In order to know as to how the seepage below the foundation of a hydraulic structure is taking place,
it is necessary to plot the flow net. In other words, we must solve the Laplacian equations. This can be accomplished either by mathematical solution of the Laplacian equations, or by Electrical analogy method, or by graphical sketching by adjusting the streamlines and equipotential lines with respect to the boundary conditions. These are complicated methods and are time consuming. Therefore, for designing hydraulic structures such as weirs or barrage or pervious foundations, Khosla has evolved a simple, quick and an accurate approach, called Method of Independent Variables.
In this method, a complex profile like that of a weir is broken into a number of simple profiles; each
of which can be solved mathematically. Mathematical solutions of flow nets for these simple standard
profiles have been presented in the form of equations given in Figure and curves given in Plate, which can be used for determining the percentage pressures at the various key points. The
simple profiles which hare most useful are:
(i) A straight horizontal floor of negligible thickness with a sheet pile line on the u/s end and d/s end.
(ii) A straight horizontal floor depressed below the bed but without any vertical cut-offs.
(iii) A straight horizontal floor of negligible thickness with a sheet pile line at some intermediate point.
The key points are the junctions of the floor and the pole lines on either side, and the bottom point of
the pile line, and the bottom corners in the case of a depressed floor. The percentage pressures at these key points for the simple forms into which the complex profile has been broken is valid for the
complex profile itself, if corrected for
(a) Correction for the Mutual interference of Piles
(b) Correction for the thickness of floor
(c) Correction for the slope of the floor
(a) Correction for the Mutual interference of Piles:-
The correction C to be applied as percentage of head due to this effect, is given by
Where,
b′ = The distance between two pile lines.
D = The depth of the pile line, the influence of which has to be determined on the neighboring pile of
depth
d. D is to be measured below the level at which interference is desired.
d = The depth of the pile on which the effect is considered
b = Total floor length
The correction is positive for the points in the rear of back water, and subtractive for the points
forward in the direction of flow. This equation does not apply to the effect of an outer pile on an
intermediate pile, if the intermediate pile is equal to or smaller than the outer pile and is at a distance less than twice the length of the outer pile.
Suppose in the above figure, we are considering the influence of the pile no (2) on pile no (1) for
correcting the pressure at C1. Since the point C1 is in the rear, this correction shall be positive. While
the correction to be applied to E2 due to pile no (1) shall be negative, since the point E2 is in the forward direction of flow. Similarly, the correction at C2 due to pile no (3) is positive and the correction at E2 due to pile no (2) is negative.
(b) Correction for the thickness of floor:-
In the standard form profiles, the floor is assumed to have negligible thickness. Hence, the percentage pressures calculated by Khosla’s equations or graphs shall pertain to the top levels of the floor. While the actual junction points E and C are at the bottom of the floor. Hence, the pressures at the actual points are calculated by assuming a straight line pressure variation.
Since the corrected pressure at E1 should be less than the calculated pressure at E1′, the correction to
be applied for the joint E1 shall be negative. Similarly, the pressure calculated C1′ is less than the corrected pressure at C1, and hence, the correction to be applied at point C1 is positive.
(c) Correction for the slope of the floor:-
A correction is applied for a slopping floor, and is taken as positive for the downward slopes, and negative for the upward slopes following the direction of flow. Values of correction of standard slopes such as 1 : 1, 2 : 1, 3 : 1, etc. are tabulated in Table
The correction factor given above is to be multiplied by the horizontal length of the slope and divided by the distance between the two pile lines between which the sloping floor is located. This correction is applicable only to the key points of the pile line fixed at the start or the end of the slope.
Exit gradient (GE):-
It has been determined that for a standard form consisting of a floor length (b) with a vertical cutoff of depth (d), the exit gradient at its downstream end is given by
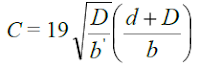









Comments
Post a Comment